Category Archives: Optical Illusions

Geometric illusions, Optical Illusions, The Poggendorff Illusion

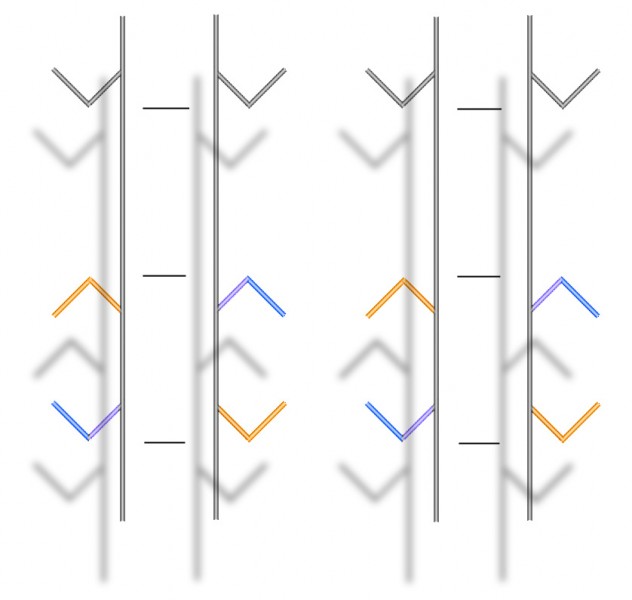
Poggendorff versus Mueller-Lyer

PoggendorffversusMueller-Lyer

This is a stereo picture-pair, but you can see what’s happening here without having to view the images in 3D if you prefer.  However,  if you’ve not got the knack, and would like to practice on this post, here’s how.  Hold up a pen about in the middle, between the two pictures, and about five inches from your eyes (careful!).  If you now try to focus on the tip of the pen, you’ll notice that the blurry image of the figure has doubled.  Now move the pen-tip away from your eyes, and notice that the two blurry middle images of the figure are beginning to overlap.  Once they overlap (probably when the pen-tip is something like ten inches away from your face), see if you can get them to overlap exactly, and then come into focus.  If that doesn’t work, try this great tutorial on another site. Or try our earlier post about stereo picture pairs.

If you’ve got it, you should see the parallel vertical bars and their attachments floating in front of a surface with their shadows thrown on it. You’ll see the same if you view the image normally, but not with the illusion of 3D.  So what’s going on?

It’s a much stronger version of some paradoxical effects I showed in an earlier post.  The tips of the arrowheads are all objectively exactly the same distance apart, as indicated by the horizontal lines aligned with them in between the vertical bars.  But that’s not how they appear if you look at the arrowheads:  the inward pointing arrows look much further apart than the outward pointing ones.  (That’s the Mueller-Lyer illusion).  But now check out the lower, coloured arrowheads.  The coloured arms that contact the vertical bars are objectively aligned, but appear not to be – the upper arm in each case seems shifted a bit upward, and the lower arm a bit downward.  (That’s the Poggendorff illusion).  For the arms to appear out of alignment like that, you’d imagine the arrowheads must move further apart.  But that’s exactly the opposite of what the Mueller-Lyer illusion is making them seem to do.

Continue reading →

Ambiguous images, Optical Illusions

Koala and Woven Person

Who's looking at who's severed head

 

Here’s another ambiguous severed head illusion.  Is Koala thoughtfully holding up the severed head of Woven Person for inspection, or is it the other way round?  You can see it both ways.  For examples of this illusion in earlier posts, check out The Screams after Munch, the Monks, and the Mask/Skull illusion.  (On that link this illusion may be at the top of the page, if so scroll down for the previous versions).

Optical Illusions, Size-constancy effects

Big Ben leaning over!

3 Comments

Big Ben

Does Big Ben look like it’s leaning over more in the right hand image than in the left hand one?  It can take a double-take to spot that the two pictures are identical. I find it a fantastically strong illusion.

It’s a demo of a new illusion found by Frederick Kingdom and colleagues (you’ll need to scroll down that link to get to their bit – look out for an even more than usual Leaning Tower of Pisa). Their discovery is a new version of the size-constancy illusion. This is my second demonstration of it – a few posts back I used a picture of a historic streetlamp. But here’s an example that looks stronger to me, with a better known subject.

Update 10 Oct 2011.  Big Ben really is leaning over! But not (yet) as much as it appears to lean in this illusion.

illusions and aesthetics, Optical Illusions, Tessellations

A tessellation pioneer

4 Comments

You probably know the tiling patterns of M.C.Escher.  But how about Koloman Moser?  Here are a couple of his designs.

Moser tilings

Moser was working in Vienna, Austria, a hundred years ago.  (He died in 1918).  I don’t know where he would have learned to do tessellating designs, that is, designs with motifs that repeat the way jigsaw puzzle pieces fit together, with no gaps or overlaps.  If you have checked out our tessellation tutorial, you’ll know that the secret of these designs is that the edge of each “tile” of the pattern must be able to be snipped into pairs of identical line segments.  Here’s how it works with Moser’s fish design.

Moser design demo

To the right you can see that the fish outline can be divided into three pairs of segments, a yellow pair, a red pair and a blue pair.  In the yellow pair, the top line is just repeated lower down to make the pair, in a move called a translation.  The red and blue pairs are a bit more complicated.  In each pair, the lower line segment is a mirror reflection of the upper segment, but shifted downwards.  That kind of shifted reflection is called a glide reflection.  It’s a fact that any motif whose edges can be snipped into one pair of segments that repeat by translation, connected as here to two parallel pairs whose edges repeat by glide reflection, will tessellate perfectly.  And that’s just one of 28 recipes for motifs that tessellate.

For a more technical account of Moser’s symmetry designs, see:

https://archive.bridgesmathart.org/2019/bridges2019-411.pdf

The author (John M.Sullivan of the Technische Universität Berlin) analyses numerous Moser designs, including the right hand design in the image at the start of the post.  He points out that, in an earlier version of this post, I got the analysis of this fascinatingly complex design wrong.

Illusion demos with animations, Optical Illusions

Position cues from a moving shadow

3 Comments

Does the ball sometimes seem to be bouncing, and moving nearer and further away?  Look again just at the track of the ball and you’ll see that all it ever does is to move diagonally from one corner of the board to the other. The spatial effects, and even the way the ball seems to accelerate at points, are all down to the moving shadow.

When the shadow sticks to the ball, the ball seems to just move across the surface and into the distance. That’s remarkable, because the ball should appear smaller with distance, but in fact the image of the ball here doesn’t change. The shadow cue is so strong it over-rides the problem. As the shadow drops to the foot of the image, the ball appears higher in the space, but nearer to us.

Once again, the effects appear even though the ball does change at all in size, as it should according to the rules of perspective – though some viewers might see an illusion of size-change, compensating for the anomalous lack of real size change.

I’ve tried to base my animation demo pretty closely on one described by Daniel Kersten and colleagues in 1997, in their celebrated original publication of this effect.

Ambiguous images, Optical Illusions

A wonky dagger illusion

Wonky dagger illusion

There’s something amiss with this dagger, for sure. For a start, the blade’s a bit short. More important, you can’t be sure just from the picture where the blade is pointing. That’s because one and the same perspective view can arise from more than one three-dimensional configuration, out there in the world.  This dagger is particularly hard to interpret.  It could be pointing downwards, with one edge of the blade longer than the other, like the blade in the top left pair of little images, of the dagger seen head on and from the side. Or the edges of the blade could be the same lengths, so we must have a steep perspective view of it leaning sideways, as in the top right hand pair of views. Look at the big image for a few moments, and I think you’ll be able to see it both ways.

Both configurations present exactly the same view in perspective, and both are about equally likely. (Well, maybe equally unlikely with this dagger would be nearer the mark). It’s a variant on an illusion which presents another clash of improbable alternatives – but one that tricks us into going for what may seem the least likely choice.  We could call it the wonky flower box illusion.

wonky flower box illusion

Do the flower boxes in this scene look like they’re rectangular, if seen from above, but sloping downwards? But what if they stick straight ahead out from wall, like well-behaved flower boxes should, but are trapezoid, seen from above, (as diagrammed to the right)? Trouble is, once again the perspective view will be the same either way. What’s curious is that in this case, most observers opt for the downward sloping view of rectangular boxes, unlikely though that would be in the real world.  Trapezoid plan boxes just seem too unlikely. It’s a version of the preference for right angles that leads us to accept incredible distortions of size in the Ames Room illusion.  If technical stuff is for you, here’s a serious analysis of the window box effect (though with balconies rather than window boxes doing the weird sloping stuff).  And if you just can’t get enough of that sort of thing, here’s a report of the same illusion in a church (also a bit on the technical side).

Geometric illusions, Optical Illusions, The Poggendorff Illusion

Padoxical illusions

morinaga's illusion

This is Morinaga’s paradox – two illusions in one, but two illusions that contradict one another. First note the vertical alignment of the arrow points. Don’t the tips of the inward pointing arrowheads, top and bottom, appear to be located just a little further inwards than the tips of the middle, outward pointing arrowheads? That could only be right if the horizontal space between the tips of the (top and bottom) inward pointing arrowheads was slightly less than the space between the tips of the (middle) outward pointing ones. But that’s not how it looks. The inward pointing arrowheads look further apart than the outward pointing ones.

In reality both judgments, of vertical alignment and of the horizontal gaps, are illusions.  The tips of the arrows are perfectly aligned vertically, and the horizontal gaps between the three sets of arrowheads are all exactly the same. That last effect is a version of the Muller-Lyer illusion.

Continue reading →

Impossible worlds (inc. staircases), Optical Illusions

Scrambled space

sqtemp1

One of surrealist painter Rene Magritte’s cleverest paintings, Carte Blanche, is of a rider in a wood, but all mixed up with the trees. I had a shot at playing with the same effects in the earlier Halloween post.  This time, I’ve tweaked up the complication with an impossible figure/ground reversal half-way up the columns, (in the manner of the impossible fork illusion – see our earlier post Outlines, objects and apertures).

A while back I tried out a similar figure/ground scenewarp in one of the picture pairs for an optical illusion cartoon story, Opticaloctopus.

Optical Illusions

Pixelated faces

1 Comment

Who’s this?

pixilated celebrity

 Yes, it’s Shakespeare!   Back in 1973 researchers Leon Harmon and Bela Julesz produced their famous Lincoln Illusion.  They demonstrated effects when an famous image of a face, such as Abraham Lincoln’s, is pixelated quite coarsely.  We can still recognise it easily if the pixelated version is either blurred (as to the right here – it’s a blurred version of the pixelated image, not of the original), or reduced in size, as if seen from a distance. Just three years after the original Scientific American article that made the effect widely known, Salvador Dali based a picture on the Lincoln image. (Michael Bach’s site shoes the original Lincoln image, the Dali picture and a clever interactive demo).

Note the tiny Shakespeare perched in the very bottom right corner of the left hand, pixelated image above.  It’s just the pixelated image reduced.  If you move away from the screen a few feet, you’ll find that the two large images of Shakespeare come to look more and more alike.  It’s odd how even small details of the face seem to appear.  If you want to try it with faces you know, I think it works best with about seventeen pixels along the longest dimension of the picture.  It does work best with an iconic, image – a photo everyone knows – rather than just a face you know.

So who have we here?

Pixelated celebs

I think you’ll have got those, but otherwise (and for more stuff) …

Continue reading →